In this work, a numerical method for moderate to high Reynolds number flows interacting with immersed boundaries is introduced. The numerical solution of fluid flow problems with thin flexible moving boundaries is motivated by the wide range of potential applications in biology and physiology. For example, the walls of the heart or lungs and swimming eels can be modeled as thin membranes embedded in a fluid. These are examples of flows with a reasonably high Reynolds number, in contrast to micro-organism and cell motion where the length scales typically reduce the Reynolds number to O(1) or less.

The method introduced here is based on the Lagrangian vortex method but generalizes it with the use of impulse elements (vortex dipoles) as a second computational variable. The impulse elements are attached to the boundaries and are used to account for the forces affecting the motion. The vortices occupy a region surrounding the boundaries and are used to account for the viscous effects via a deterministic diffusion method. These are schemes in which the vortex strengths, rather than the location of the particles, are changed at every time step to simulate diffusion. This type of diffusion scheme can be used while maintaining the Lagrangian character of the overall method. Various types of deterministic methods exist but many make use of similar cutoff functions and only differ in the way they approximate the Laplacian operator. We chose to use Fishelov's method since it lends itself more naturally for the purposes of this work; however, it is not the only available choice. The grid-free character of the method has the desirable property of introducing little numerical dissipation and remaining stable when decreasing values of viscosity are used.

For more information, refer to A Vortex/impulse Method for Immersed Boundary Motion in High Reynolds Number Flows

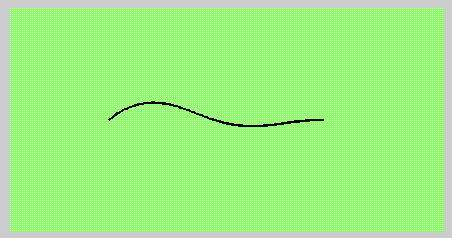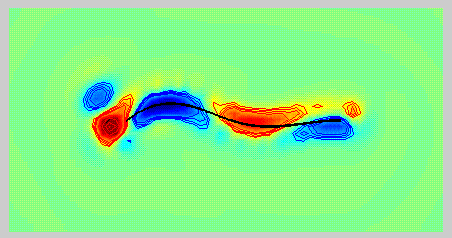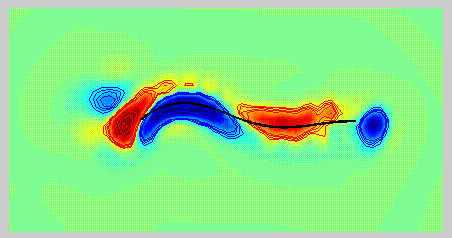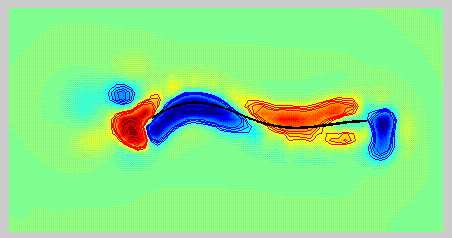
Vorticity contours surrounding an undulating filament, simulating swimming. Blue contours are of negative vorticity and red contours are of positive vorticity.