Lagrangian Vortex/Impulse Method
by Ricardo Cortez
A Lagrangian method that combines vortices and impulse elements (vortex dipoles)
is introduced. The applications addressed are flows induced by the motion of thin
flexible boundaries immersed in a two-dimensional incompressible fluid.
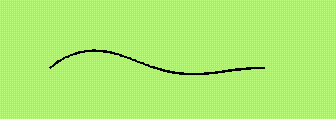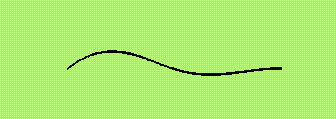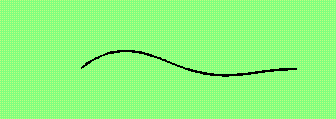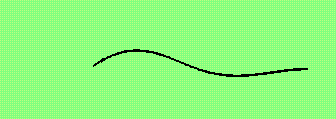
An example is an undulating filament simulating the swimming of an organism in
a slightly viscous fluid.
The impulse elements are attached to the boundaries and are used to account for
the forces affecting the motion. The vortices occupy a region surrounding the
boundaries and are used to account for the viscous effects via a deterministic
diffusion method.
Regularized Stokeslets
by Ricardo Cortez
This is a numerical method for computing Stokes flows in the presence of immersed
boundaries and obstacles. The method is based on the smoothing of the forces,
leading to regularized Stokeslets. The resulting expressions provide the pressure
and velocity field as functions of the forcing. The latter expression can also be
inverted to find the forces that impose a given velocity boundary condition.
The numerical examples presented demonstrate the wide applicability of the method
and its properties. Solutions converge with second-order accuracy when forces are
exerted along smooth boundaries. Examples of segmented boundaries and forcing at
random points are also presented.